常用三种加速老化|第三方检测机构
更新:2025-02-05 08:30 编号:20595398 发布IP:113.104.201.3 浏览:339次
- 发布企业
- 深圳市讯科标准技术服务有限公司-精英部商铺
- 认证
- 资质核验:已通过营业执照认证入驻顺企:第4年主体名称:深圳市讯科标准技术服务有限公司组织机构代码:91440300MA5D902695
- 报价
- 请来电询价
- 关键词
- 检测 认证 职业卫生 第三方 产品检测 机构 噪音 环境 可靠性
- 所在地
- 深圳市宝安区航城街道九围社区洲石路723号强荣东工业区E2栋二楼
- 联系电话
- 13352906691
- 陈工
- 13352906691
- 业务咨询
- 陈树泽 请说明来自顺企网,优惠更多
详细介绍
1. 只考虑热加速因子的阿伦纽斯模型( Arrhenius Mode)
某一环境下,温度成为影响产品老化及使用寿命的主要因素时,采用单纯考虑热加速
因子效应而推导出的阿伦纽斯模型来描述测试,其预估到的结果会更接近真实值,模拟试验的
效果会更好。此时,阿伦纽斯模型的表达式为:
![]()
式中:
AF 是加速因子;
Ea 是析出故障的耗费能量,又称激活能。不同产品的激活能是不一样的。一般来说,激活
能的值在 0.3ev~1.2ev 之间;
K 是玻尔兹曼常数,其值为 8.617385 × 10 ^-5;
Tu 是使用条件下 非加速状态下 的温度值。此处的温度值是温度值,以 K( 开尔文)作单
位;
Tt 是测试条件下 加速状态下 的温度值。此处的温度值是温度值,以 K( 开尔文)作单位。
案例:
某一客户需要对产品做 105℃的高温测试。
据以往的测试经验,此种产品的激活能Ea 取0.68 。
对产品的使用寿命要求是 10年,现可供测试的样品有 5个。若对5个样品进行测试,需测试多长时间才能满足客户要求?
已知的信息有 Tt 、 Ea ,使用的温度取25 ℃,则先算出加速因子 AF
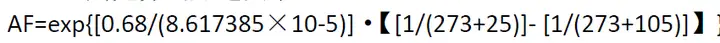
Zui终:
AF≈271.9518
又知其目标使用寿命:
L 目标 =10years=10 × 365 × 24h=87600h
故即可算出
L 测试 = L 目标 /AF=87600/271.9518h=322.1159h≈323h
现在 5 个样品进行测试,则测试时长为:
LZui终 =323/5h=65h
这即是说明,若客户用 5 个产品在 105 ℃高温下测试65h 后产品未发生故障,则说明
产品的使用寿命已达到要求。
通过这个案例可以看出,利用阿伦纽斯模型可以提前预估测试的相关信息,指导客户该怎样进行测试才既能达到目标值而又Zui大限度的降低成本。
本案例中,若客户急需测试结果,那么可以投入 10个或者更多的样品来缩短整个测试时长;或者在允许的情况下提高温度,加快完成测试。根据需求灵活的调整测试方案,这才能更完美地达到目标,提高工作效率,省去一些不必要的费用。
2.综合温度及湿度因素的阿伦纽斯模型(Arrhenius Mode With Humidity)
综合温度及湿度因素的阿伦纽斯模型的表达式为:
![]()
式中:
AF是加速因子;
Ea是析出故障的耗费能量,又称激活能。不同产品的激活能是不一样的。一般来说,激活是析出故障的耗费能量,又称激活能。激活能的值在能的值在0.3ev~1.2ev之间;
K是玻尔兹曼常数,其值为8.617385×10-5;
Tu是使用条件下是使用条件下(非加速条件下)的温度值。此处的温度值是温度值,以K(开尔文开尔文)作单作单位;
Tt是测试条件下是测试条件下(加速条件下)的温度值。此处的温度值是温度值,以K(开尔文开尔文)作单位;
RHu是使用条件下(非加速状态下)的相对湿度值;
RHt 是测试条件下(加速状态下)的相对湿度值。
模型二可以说是模型一的拓展,它只是在模型一的基础上简单地添加了湿度这一影响因素。
长期以来的测试经验表明,用模型二来解释某些情况下湿度对加速测试的影响并不准确。
一种更为准确的综合考虑温湿度影响的模型将被提出,这即是下文将介绍的一种模
型 Hallberg Peck 模型。
3.Hallberg Peck 模型
Hallberg Peck模型综合考虑了温度、湿度影响,它相比于模型二更能准确的描述在温湿度条件下进行的老化测试,其表达式为:
![]()
式中:
AF 是加速因子;
Ea 是析出故障的耗费能量,又称激活能。不同产品的激活能是不一样的。一般来说,
激活能的值在 0.3ev~1.2ev 之间;
K 是玻尔兹曼常数,其值为 8.617385 × 10^-5
Tu 是使用条件下 非加速条件下 的温度值。此处的温度值是温度值,以 K( 开尔文
作单位;
Tt 是测试条件下 加速条件下 的温度值。此处的温度值是温度值,以 K( 开尔文 作
单位;
RHu 是使用条件下 非加速状态下 的相对湿度值;
RHt 是测试条件下 加速状态下的相对湿度值。
案例:
某一半导体元件生产厂家,经过长期研究开发出一款新产品。
初步将新产品的MTBF 定为 20 年。
新产品日常的使用环境为 45℃25%RH 。
为了验证 其使用寿命是否达到要求,厂家要把新产品置于 85℃85%RH 的高温高湿条件下做加速测试。
现客户共有 3 款新产品,仅 2 款可用于测试,剩余一款作为其余两款试验后对比之用。
厂家现在希望能Zui快地完成测试,得到相关结果,那这一Zui快时间是多少?
现在Zui多只能用 2 个产品进行测试,则测试时长为: T Zui终 =76/2h=38h
这即是说明,若客户想得到Zui快的测试结果需用 2 个产品进行 85 85%RH 的高温高湿测试 38h,若之后产品未发生故障,则可说明其 MTBF 已达目标。
综合以上三个模型可以看出,他们都有一些共通的参数,如 Ea 、 k 、 Tu 、 Tt ,其中 k 是一恒量,其值始终不会变,变化的是 Ea 、 Tu 、 Tt Tu 和 Tt 是人为设定的,它的变化有很强的随机性。而 Ea则不同,它是析出故障所耗费的能量,当故障具体到某一种特定类型时,其值会在很小的范围内产生波动,几乎可认为不变。
以下是一些常见故障的 Ea 值:
氧化膜破坏: 0.3ev
离子性( Si02 中 Na 离子漂移) 1.0 1.4ev
离子性(Si-SiO2 界面的慢陷阱) 1.0ev
电迁移造成短路或开路 0.6ev
铝腐蚀 0.6——0.9ev
金属间化合物生长 0.5——0.7ev
其它Ea值可参考GR268标准内规定数据。
| 注册资本 | 100 | ||
| 主营产品 | 有害物质检测,安规检测,EMC检测,环境安全检测,电子电器产品可靠性与失效分析,材料可靠性与失效分析,金属材料、非金属材料分析,纺织品、鞋类、皮革检测,玩具产品检测,建材与轻工产品检测,汽车整车及其零部件检测,食品、药品、化妆品、饲料及食品包装和接触材料检测,验货与合规服务,审核服务,计量校准及仪器销售,半导体及相关领域检测分析等多项综合检测与认证服务。 | ||
| 经营范围 | 产品检测认证 | ||
| 公司简介 | 深圳市讯科标准技术服务有限公司是一家依据ISO/IEC17025运行的第三方检测机构。我检测中心在工业品、消费品、贸易保障及生命科学四大领域,提供有害物质检测,安规检测,EMC检测,环境安全检测,电子电器产品可靠性与失效分析,材料可靠性与失效分析,金属材料、非金属材料分析,纺织品、鞋类、皮革检测,玩具产品检测,建材与轻工产品检测,汽车整车及其零部件检测,食品、药品、化妆品、饲料及食品包装和接触材料 ... | ||
- 工业机器人MTBF测试方法机器人在现代工业中扮演着不可或缺的角色,因其高效、精准的特性而备受欢迎。而在机器... 2024-06-07
- 环境适应性试验报告-国军标GJB检测机构环境适应性试验是考核产品在各类气候环境以及机械环境条件试验下,产品是否可以正常运... 2024-06-07
- 国军标GJB150可靠性试验检测机构国军标150可靠性试验检测服务GJB367军用通信设备型式试验、军用计算机装备G... 2024-06-07
- 环境与可靠性试验标准介绍,GB、GJB、MIL 环境试验与可靠性试验虽然关系紧密,但它们在试验目的,所用环境应力数量,环境力量值... 2024-06-07
- LED第三方检测机构检测报告 LED显示屏户外第三方检测机构质检报告LED显示屏户外CNAS报告LED显示屏检... 2024-06-07


